Rigid body transformation refers to how a solid object moves in space through rotation and translation without deforming. Whether it’s the movement of a robotic arm, the motion of a satellite, or rendering objects in computer graphics, rigid body transformations are foundational in mechanics and robotics.

In this article, we’ll explore the building blocks of rigid body transformation, including screw motion, twists, and wrenches, and the role of coordinate transformations in connecting multiple perspectives of movement. This exploration will include essential math to help clarify these concepts.

Mathematical Foundations of Rigid Body Transformation

A rigid body transformation combines rotation and translation into a seamless movement. This transformation is often expressed using matrices that make it easier to handle multiple operations together.

Rotation Matrices and Translation Vectors

![[Rigid Body Transformation-20241019174137671.webp]]

• Rotation matrix $R \in \mathbb{R}^{3 \times 3}$ : Describes how an object rotates around an axis.
• Translation vector $t \in \mathbb{R}^3$: Describes how far an object shifts along the X, Y, and Z axes.

The combined transformation of a point $\mathbf{p}$ in 3D space can be expressed as:

$\mathbf{p}’ = R \mathbf{p} + t$

Here, $\mathbf{p}’$ is the new position of the point after applying the transformation.

However, managing multiple transformations is easier with homogeneous coordinates, which combine rotation and translation into a single 4x4 transformation matrix:

$T = \begin{pmatrix} R & t \ 0 & 1 \end{pmatrix}$

Applying this matrix to a point $\mathbf{p} = (x, y, z, 1)^T$ gives:

$\mathbf{p}’ = T \mathbf{p}$

Coordinate Transformations Between Frames

Why Coordinate Transforms Matter

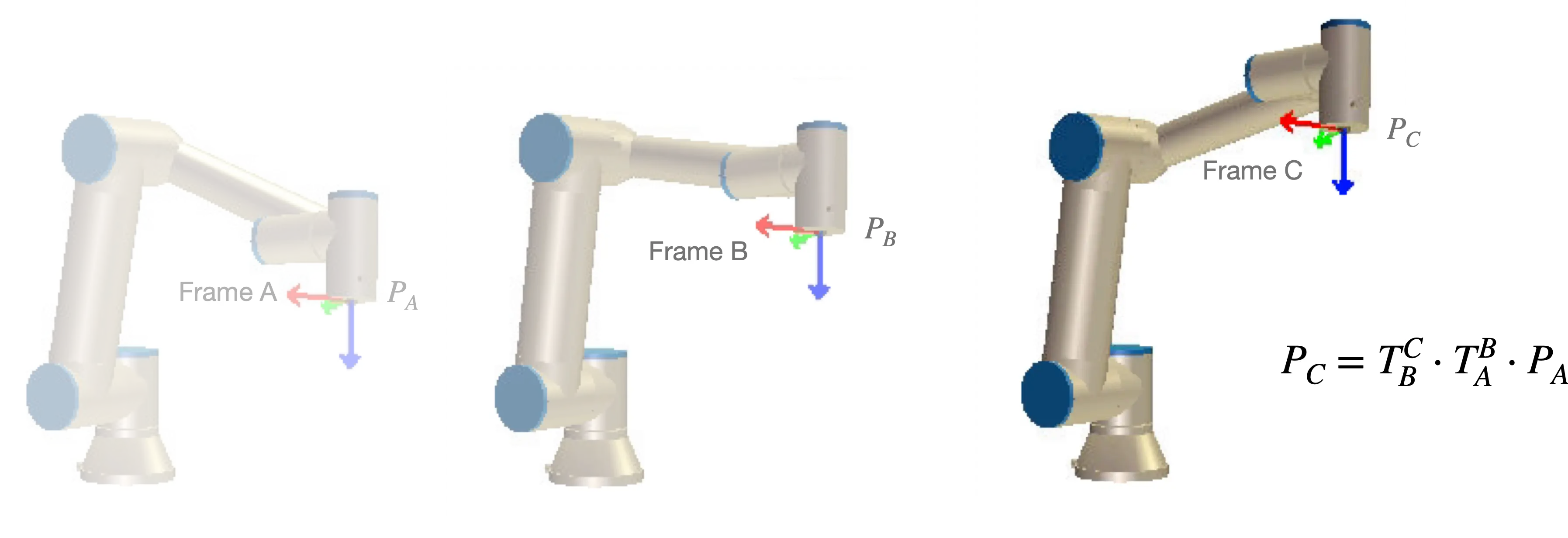
In real-world applications, objects often move relative to different coordinate systems, or frames of reference. For example, a robotic arm may have one frame fixed to its base and another on its hand (the end effector). To properly describe motion, we use coordinate transformations to express the same movement across these frames.

Given a rigid body transformation from Frame A to Frame B: ![[Rigid Body Transformation-20241019174433219.webp]]

$\mathbf{p}_B = T^B_A \mathbf{p}_A$

Here, $T_{A}^B$ is the transformation matrix that relates the coordinates in Frame A to those in Frame B. If the body continues to move, multiple transformations can be concatenated by multiplying matrices:

$T_{C}^A = T_{B}^A \cdot T_{C}^B$

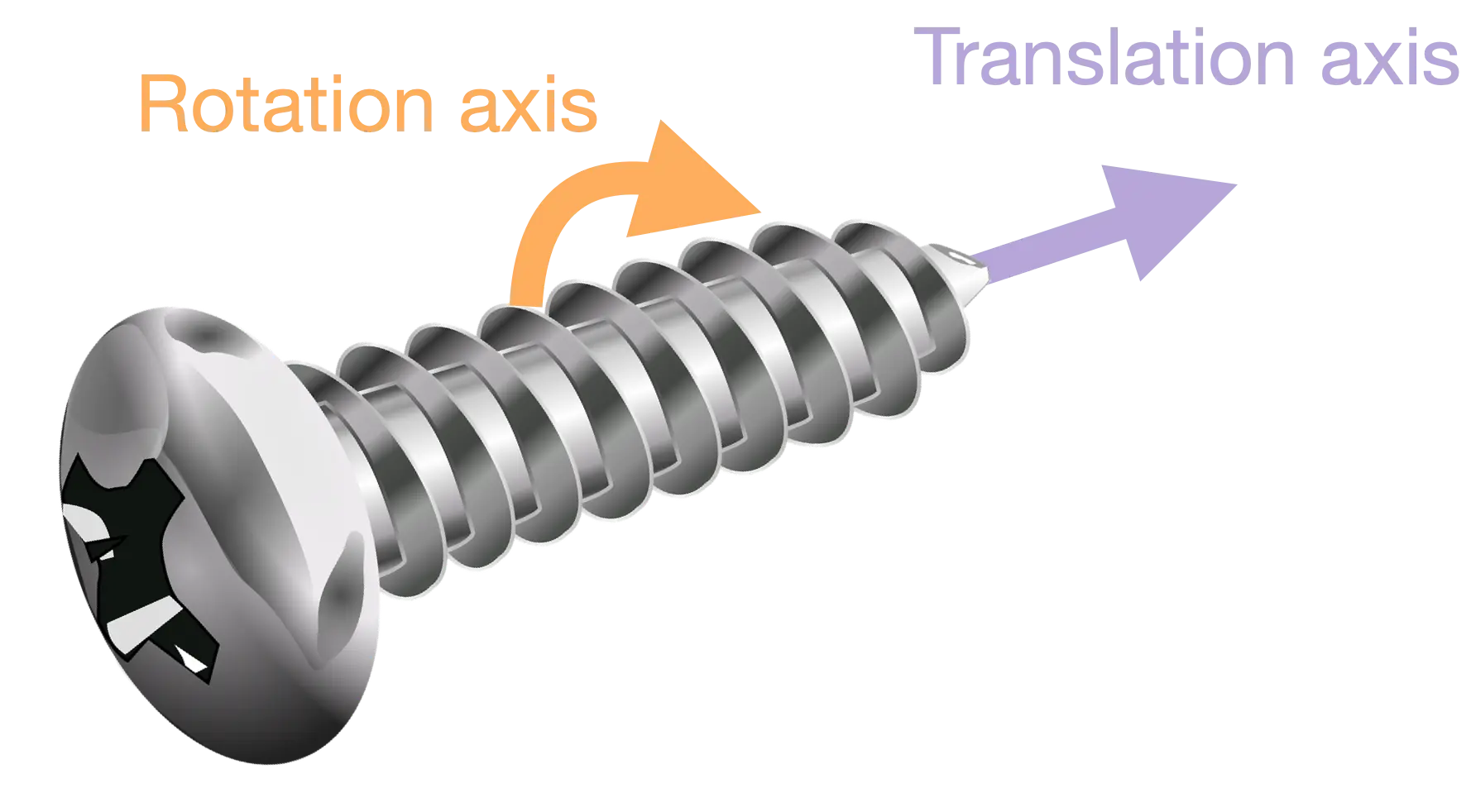
Screw Motion: Combining Rotation and Translation

Screw motion elegantly describes movement where an object both rotates around an axis and translates along the same axis—just like a screw advancing through a nut. The general equation for screw motion is: ![[Rigid Body Transformation-20241019174628785.webp]]

$\mathbf{p}(t) = R(t) \mathbf{p}_0 + t \mathbf{v}$

where $R(t)$ is the rotation matrix describing how the object rotates with time $t$, and $\mathbf{v}$ is the direction of translation.

The beauty of screw motion lies in its ability to express combined rotation and translation through a single screw axis. In fact, many robotic movements—like the motion of a robotic gripper or a drilling tool—can be modeled using screw motion.

Twist: Mathematical Representation of Instantaneous Motion

A twist compactly describes the instantaneous motion of a rigid body, combining both angular velocity and linear velocity into a 6-dimensional vector. This is especially useful when controlling robotic arms or vehicles.

Definition of a Twist

The twist $\xi$ is given by:

$\xi = \begin{pmatrix} \omega \ v \end{pmatrix}$

where:

• $\omega \in \mathbb{R}^3$ is the angular velocity vector.
• $v \in \mathbb{R}^3$ is the linear velocity vector.

The twist captures how fast a body is rotating and moving at any given moment. In practice, it is used for motion control in robotics, helping determine how fast an end-effector needs to move and rotate to reach a target position.

Example Application:
Imagine a robotic arm that needs to place a glass on a table. The twist helps control both the speed at which the arm reaches the table and the rotation required to properly orient the glass.

Wrench: Forces and Torques Acting on a Rigid Body

While a twist describes motion, a wrench captures the forces and torques acting on the rigid body. In robotics, wrenches are essential for determining how much force a robot’s gripper needs to apply to hold or move an object.

Definition of a Wrench

The wrench $W$ is represented as:

$W = \begin{pmatrix} \tau \ f \end{pmatrix}$

where:

• $\tau \in \mathbb{R}^3$ is the torque vector.
• $f \in \mathbb{R}^3$ is the force vector.

For a given twist $\xi$, the power exerted by a wrench $W$ is:

$P = W^T \xi$

This equation helps calculate how much power is required to maintain a specific motion under applied forces and torques.

Bringing It All Together: Screw Motion, Twist, and Wrench

In real-world applications, screw motion, twists, and wrenches work in harmony to model and control complex rigid body movements. Consider a robotic arm:

• Twists describe the desired velocity of the arm’s motion.
• Wrenches describe the forces and torques the arm needs to apply.
• Screw motion ensures smooth, coordinated movement by combining rotation and translation along the same axis.

These mathematical tools help engineers design smooth, efficient movements while also ensuring the right amount of force is applied.

Conclusion: The Mathematical Backbone of Rigid Body Transformations

Rigid body transformations—whether expressed through coordinate transforms, twists, wrenches, or screw motion—provide a complete framework for understanding motion and forces in 3D space. These concepts are indispensable for fields like robotics, aerospace, computer graphics, and biomechanics.

By combining rotation, translation, forces, and torques into concise mathematical models, we can control complex systems with precision. Whether it’s programming a robot to assemble a product or simulating spacecraft maneuvers, rigid body transformations ensure seamless, reliable motion.

Disclosure:
This article includes content generated with the assistance of large language models (LLMs). The generated sections have been reviewed and refined to ensure accuracy and alignment with the topic.